图

定义

一个无向图 $G$ 由顶点集合 $V(G)$ 和边集合 $E(G)$ 组成，其中 $V(G)$ 是有限非空集合，元素称为结点； $E(G)$ 是 $V(G)$ 的无序对(若为有向图，则是有序对)的集合，且不重复（非多重图）。

*:下文中，如无特殊说明，均指无向简单图。

常用表示

$G$ 的阶 $n$ 是顶点的个数。

$G$ 的边数 $m$ 是边的个数。

若 $e=uv$ 是 $G$ 中的一条边，则称 $u$ 和 $v$ 是相互邻接的，边 $e$ 分别与 $u$ 和 $v$ 相互关联。

推广

简单图：即上述定义，最基本的图。

多重图：边可以重复，即 $E(G)$ 可以重复。

伪图：在多重图的基础上，允许顶点关联自己，即 $e=uu$ 。

度

点度： $d_G(u)$ :点 $u$ 的关联的边的个数，环算作两条边。

孤立结点：度为0的结点

缩写

	度	最大点度	最小点度
$\text{全称}$	$d_G(u)$	$\Delta_G$	$\delta_G$
$\text{abbr}$	$d(u)$	$\Delta$	$\delta$

对于有向图

度	最大出度	最大入度	最小出度	最小入度
$d(u)$	$\Delta^+$	$\Delta^-$	$\delta^+$	$\delta^-$

握手定理

\sum_{u\in G}d(u)=2m

推论：计数度的结点个数为偶数

图的分类

零图：只由孤立节点构成，即 $G=(V,\empty)$ $G = (V, \emptyset)$
- 平凡图：只由一个孤立节点构成
正则图：所有结点的度都相等。点度为 $k$ $k$ 的正则图称为 $k$ $k$ 度正则图
- 完全图：所有结点的相互邻接，是 $n-1$ 度正则图
二部图：结点分为两个集合 $X,Y$ $X, Y$ ，且不相交( $X\cap Y=\empty$ $X \cap Y = \emptyset$ )，且 $X$ $X$ 和 $Y$ $Y$ 内部的结点都没有边相连，且任意边的两个端点分别属于 $X$ $X$ 和 $Y$ $Y$
- 完全二部图： $X$ 和 $Y$ 中的结点全部邻接，若 $|X|=n_1,|Y|=n_2$ ，记为 $K_{n_1\cdot n_2}$

推论：正则图的点度为奇数的充要条件是 $n$ 为奇数

For 有向图

有向完全图：每对结点 $u,v$ 有边 $uv$ 和 $vu$
竞赛图：每对结点 $u,v$ 恰有一条边 $uv$ 或 $vu$

子图

$G=(V_1,E_1),H=(V_2,E_2)$

$H$ 是 $G$ 的（ <? extends 子图>）

子图： $V_2\subseteq V_1,E_2\subseteq E_1$ $V_{2} \subseteq V_{1}, E_{2} \subseteq E_{1}$
- 生成子图： $V_2=V_1$
- 真子图： $V_2\subset V_1 \text{ or } E_2\subset E_1$
- 平凡子图： $V_1=V_2,(E_2=E_1 \text{ or } E_2=\empty)$

产生子图的方法

删点子图： $G-u$ $G - u$ 表示 $G$ $G$ 删去点 $u$ $u$ 与 $u$ $u$ 邻接的边
- 删点子图（删点集）： $G-S$ 表示 $G$ 删去点集 $S$ 与 $S$ 中结点所有邻接的边
删边子图： $G-e$ $G - e$ 表示 $G$ $G$ 删去边 $e$ $e$
- 删边子图（删边集）： $G-E$ 表示 $G$ 删去边集 $E$
诱导子图：
- 点诱导子图： $\text{For }S\subseteq V,E'=\{uv|u,v\in S\land uv \in E\}$
- 边诱导子图： $\text{For }\emptyset\neq T\subseteq E,V'=\{u|u\in T\text{中含有的点}\}$

补图

$G=\{V,E\},G'=\{V',E'\}$

若（以下条件均等价）

$V=V'$ , $\land (E\cap E'=\emptyset\land E\cup E'=\{uv|u,v\in V\})$
$V=V'$ , $E'=\{uv|v,u\in V\land uv\notin E\}$
$V=V'$ , $uv\in E'$ 当且仅当 $uv\notin E$
$V=V'$ , $G$ 与 $G'$ 边相加恰好构成 $V$ 的完全图

则称 $G$ 和 $G'$ 互为补图

通路与回路

基本定义

道路：非空序列 $P=v_0e_1v_1\cdots e_kv_k$

$v_0$ 是起点
$v_k$ 是终点
其余结点是内部结点

零道路： $P=v_0$

闭道路： $v_0\neq v_k$ /开道路： $v_0=v_k$

简单道路： $P$ 中边不重复（闭道路称为回路）

基本道路： $P$ 中点不重复（闭道路称为圈，按照长度分为奇卷/偶圈）

连通性

支

$\omega(G)$ ：极大连通子图

$\omega(G)=1$ :连通图

$\omega(G)>1$ :非连通图

距离

非负/对称/满足三角不等式

割集

割点 $v$ ： $G-v$ 不是连通图
割集 $S$ ： $G-S$ 不是连通图
基本割集 $S$ ：若 $S'\subset S$ ，则 $G-S'$ 是连通图；换句话说，基本割集 $S$ 应当看成一个基本单位，取其子集无法将图 $G$ 分成非连通图。

显然，割点 $v$ 的集合 $\{v\}$ 是基本割集。

基本割集也是割集。

割边

定于与割点类似

割边 $e$ ： $G-e$ 不是连通图
割边集 $E$ ： $G-E$ 不是连通图
基本割边集 $E$ ：若 $E'\subset E$ ，则 $G-E'$ 是连通图；换句话说，基本割边集 $E$ 应当看成一个基本单位，取其子集无法将图 $G$ 分成非连通图。

连通度

点连通度 $\kappa(G)$ ： $G$ 删点使其成为非连通的/一个结点的子图，所需的最少结点数。
边连通度 $\lambda(G)$ ： $G$ 删边使其成为非连通的/一个结点的子图，所需的最少边数。

连通/边连通

$k$ 连通： $\kappa(G)\geq k$
$k$ 边连通： $\lambda(G)\geq k$

定理

$\kappa(G)\leq\lambda(G)\leq\delta$

有向图

单向连通： $G$ 中任意两点，至少在一个方向上连通
强连通： $G$ 中任意两点，在两个方向上都连通
弱连通：基图（去掉边的方向）是连通图

$强连通\Rightarrow 单向连通 \Rightarrow 弱连通$

强分图：极大强连通子图
单向分图：极大单向连通子图
弱分图：极大弱连通子图

定理（简单有向图）

一个简单有向图是强连通的 $\iff$ 有一条包含所有结点的有向闭道路
每个结点位于且仅位于一个强分图中

矩阵表示

邻接矩阵 $A_{n\times n}$

这部分对有向图与无向图均成立

a_{ij}=\left\{\begin{aligned} &1 & \text{when}(v_i,v_j)\in E\\ &0 & \text{when}(v_i,v_j)\notin E\\ \end{aligned}\right.

幂次方含义

由矩阵的相乘关系可知

a_{ij}^{(2)}=\sum_{k=1}^na_{ik}a_{kj}

就是说， $a_{ij}^{(2)}$ 表示从 $v_i$ 到 $v_j$ 的长度为 $2$ 的路径的个数。

更进一步， $a^{(n)}_{ij}$ 表示从 $v_i$ 到 $v_j$ 的长度为 $n$ 的路径的个数。

推论

最小的 $k$ 使得 $a_{ij}^{(k)}>0$ ，这个 $k$ 就是 $v_i$ 到 $v_j$ 的最短路径长度
若对 $k\in[1,\cdots ,n-1]$ ， $a_{ij}^{(k)}=0$ ，则 $v_i$ 到 $v_j$ 是不可达的
若存在 $t,s:a_{ij}^{(t)}>0\land a_{ji}^{(s)}>0$ $\iff$ $G$ 含包含 $v_i$ 和 $v_j$ 的有向回路
$B_k=\sum_{i=1}^k A^i$ ，则 $B_k$ 元素 $b_{ij}^{(k)}$ 代表从 $v_i$ 到 $v_j$ 的长度不超过 $k$ 的路径的个数。

可达性矩阵 $P$

p_{ij}=\left\{\begin{aligned} &1 & \text{when}(v_i,v_j)\text{可达}&\\ &0 & \text{when}(v_i,v_j)\text{不可达}&\\ \end{aligned}\right.

构造

传统派

利用 $B_k|_{k=n}$

构造 $\text{element-wise}$ 映射函数

p_{ij}=\left\{\begin{aligned} &1 & \text{when }b_{ij}^{(n)}>0\\ &0 & \text{when }b_{ij}^{(n)}=0\\ \end{aligned}\right.

维新派

利用 $\text{Warshall}$ 算法（略）

应用：求全部强分图

求 $P\odot P^T$ ：元素 $(P\odot P^T)_{ij}$ 表示 $v_i,v_j$ 两两是否相互连通

注意：由于点的连通实际上是自反的，因此最后还要加上单位矩阵 $I$ 。

eg.

P\odot P^T=PP^T+I=\left[\begin{matrix} 1 & 1 & 1 & 1 & 0 & 0\\ 1 & 1 & 1 & 1 & 0 & 0\\ 1 & 1 & 1 & 1 & 0 & 0\\ 1 & 1 & 1 & 1 & 0 & 0\\ 0 & 0 & 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 0 & 0 & 1\\ \end{matrix}\right]

显然，共有 $3$ 个强分图， $\{v_1,v_2,v_3,v_4\},\{v_5\},\{v_6\}$

*:矩阵元素类型为 $0/1$ 即布尔型

关联矩阵 $M_{n\times m}$

m_{ij}=\left\{\begin{aligned} &1 & \text{when }e_j\text{是}v_i\text{出边}\\ -&1 & \text{when }e_j\text{是}v_i\text{入边}\\ &0 & \text{otherwise}\\ \end{aligned}\right.

圈矩阵 $C_{c\times m}$

找出所有的圈，对于每个圈，任意指定一个正方向（顺时针/逆时针）。
其中

c_{ij}=\left\{\begin{aligned} &1 &\text{when $c_i$与$e_j$方向一致}\\ -&1 &\text{when $c_i$与$e_j$方向相反}\\ &0 &\text{when $c_i$不包含$e_j$}\\ \end{aligned}\right.

结论

CM^T=0

平面图

定义

若 $G$ 存在一种表示，使得其能被画在平面上，且点不重合，任意两条边不相交（更严谨地说是不在公共结点以外的地方相交）。

定理

若 $G$ 是平面图，则 $G$ 的任意子图也是平面图
若 $G$ 是不是平面图，则 $G$ 的任意母图也不是平面图
$K_n(n\geq 5),K_{3,n}(n\geq 3)$ 都不是平面图

面

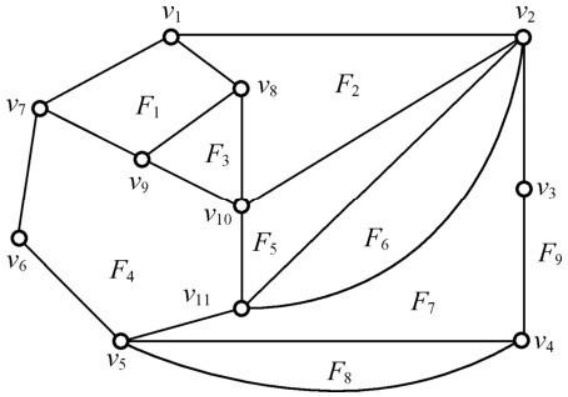
值得注意的是，在图像外部也存在一个面。如上图所示 $F_9$ 。

面度

包围这个区域的边数。注意割边要算作两次。

握手定理？

\sum \deg(F_i)=2m

欧拉公式

对于面数为 $f$ 的连通平面图 $G$ 有

n-m+f=2

推论：具有多个支的图的欧拉公式

n-m+f=1+\omega(G)

推论：平面图的必要性

m\leq 3n-6

进一步，还能推出：对于任意简单连通平面图，至少存在一个度数不超过5的节点。

圈长 $g$

其包含的最短圈的长度。如果无圈，认为其圈长为无穷大。

圈长与平面图的必要性

对上述平面图必要性再进行推广，有：

m\leq \frac{gn-2g}{g-2},(g\geq 2)

判断平面图：细分

//TODO

对偶图

//TODO

欧拉图

$G$ 是一个无向图，包含 $G$ 的每条边的简单道路称为欧拉道路。
包含 $G$ 的每条边的简单回路称为欧拉回路。
具有欧拉回路的图称为欧拉图。

欧拉图，简而言之：能不重复地一笔将整个图画完。

条件（无向图）

连通图 $G$ 是欧拉图，iff , $G$ 不含奇度数结点

非平凡连通图 $G$ 含欧拉道路，iff, $G$ 最多有两个奇度数结点

条件（有向图）

连通图 $G$ 是欧拉图，iff, $G$ 的每个结点的入度等于出度

连通有向图含欧拉道路，iff, $G$ 最多有两个结点入度不等于出度（且一个入读比出度多一，一个入读比出度少一）。

哈密顿图

哈密顿道路：包含 $G$ 的每个结点的简单道路

哈密顿回路：包含 $G$ 的每个结点的圈

含有哈密顿圈的图称为哈密顿图。

充分条件（不是必要）

对于 $n$ 阶简单图 $G$ .任意一对结点 $u,v$ 满足 $d(u)+d(v)\geq n$ ，则 $G$ 必然含有哈密顿圈

对于 $n>3$ 阶简单图 $G$ .任意一对结点 $u,v$ 满足 $d(u)+d(v)>n$ ，则 $G$ 必然是哈密顿图

闭包

若存在不相邻结点 $u,v$ ，使得 $d(u)+d(v)\geq n$ ，则构造图 $G+uv$ 。

重复上述过程直至找不到这样的结点。

闭包与哈密顿图

一个简单图 $G$ 是哈密顿图，iff， $G$ 的闭包是哈密顿图。